The Parton-Hadron-String Dynamics (PHSD) is a microscopic off-shell transport approach for the description of strongly interacting hadronic and partonic matter in and out-of equilibrium. It is based on the solution of Kadanoff–Baym equations in first-order gradient expansion in phase space which allows to describe in a causal way the time evolution of nonperturbative interacting systems. The PHSD consistently describes the full evolution of a relativistic heavy-ion collision from the initial hard scatterings and string formation through the dynamical deconfinement phase transition to the quark-gluon plasma as well as hadronization and to the subsequent interactions in the hadronic phase. The PHSD has been developed by the Giessen/Frankfurt groups on the basis of the Hadron-String Dynamics transport approach (HSD).
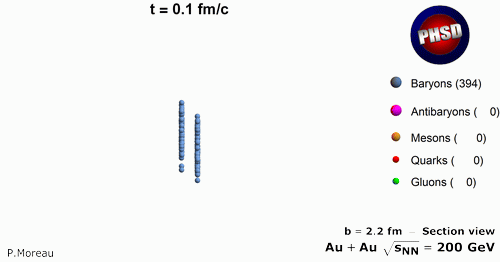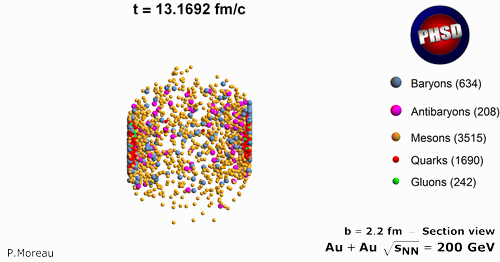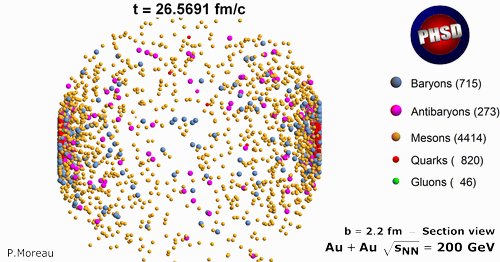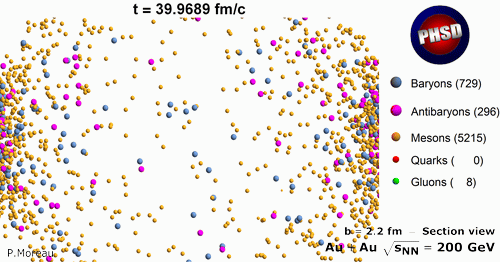
In PHSD the transition from the partonic (quarks and gluons) to hadronic degrees of freedom is described by covariant transition rates for the fusion of quark-antiquark pairs to mesonic resonances or three quarks (antiquarks) to baryonic states, i.e., by a dynamical hadronization obeying flavor current-conservation, color neutrality as well as energy-momentum conservation. The two-particle correlations resulting from the finite width of the parton spectral functions are taken into account dynamically in the PHSD by means of the generalized off-shell Cassing-Juchem transport equations for testparticles - followed from Kadanoff–Baym equations - that go beyond the mean field or Boltzmann approximation.
The transport theoretical description of quarks and gluons in the PHSD is based on the Dynamical Quasi-Particle Model (DQPM) for partons that is constructed to reproduce lattice QCD (lQCD) results for a quark-gluon plasma in thermodynamic equilibrium. The DQPM provides the mean-fields for gluons/quarks and their effective 2-body interactions that are implemented in the PHSD. Since the dynamical quarks and antiquarks become very massive close to the phase transition, the formed resonant 'pre-hadronic' color-dipole states (q-qbar or qqq) are of high invariant mass, too, and sequentially decay to the groundstate meson and baryon octets. Accordingly, the dynamical hadronization process increases the total entropy such that the second law of thermodynamics is fulfilled.
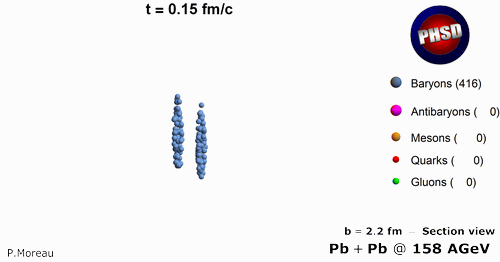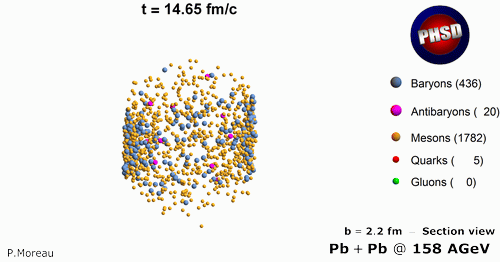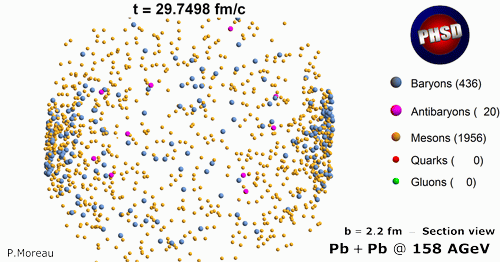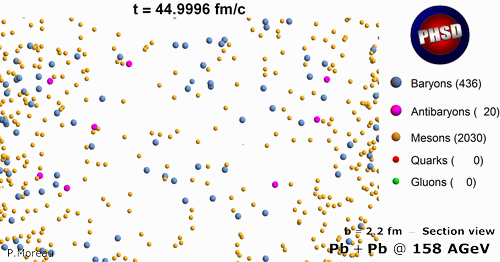
We have also studied equlibrium properties of the QGP by performing PHSD calculations in a finite box with periodic boundary conditions for fixed temperature T. In particular we find that the ratio of the shear viscosity to entropy density from PHSD shows a minimum (with a value of about 0.1) close to the critical temperature Tc=160 MeV, while it approaches the perturbative QCD (pQCD) limit at higher temperatures in line with lattice QCD results. This indicates that the QGP shows the properties of a strongly interacting liquid (sQGP) rather than —as expected initially— a weakly interacting gas of partons.